This page was generated from examples/cd_mmd_keops.ipynb.
Scaling up drift detection with KeOps
Introduction
A number of convenient and powerful kernel-based drift detectors such as the MMD detector (Gretton et al., 2012) or the learned kernel MMD detector (Liu et al., 2020) do not scale favourably with increasing dataset size \(n\), leading to quadratic complexity \(\mathcal{O}(n^2)\) for naive implementations. As a result, we can quickly run into memory issues by having to store the \([N_\text{ref} + N_\text{test}, N_\text{ref} + N_\text{test}]\) kernel matrix (on the GPU if applicable) used for an efficient implementation of the permutation test. Note that \(N_\text{ref}\) is the reference data size and \(N_\text{test}\) the test data size.
We can however drastically speed up and scale up kernel-based drift detectors to large dataset sizes by working with symbolic kernel matrices instead and leverage the KeOps library to do so. For the user of \(\texttt{Alibi Detect}\) the only thing that changes is the specification of the detector’s backend, e.g. for the MMD detector:
from alibi_detect.cd import MMDDrift
detector_torch = MMDDrift(x_ref, backend='pytorch')
detector_keops = MMDDrift(x_ref, backend='keops')
In this notebook we will run a few simple benchmarks to illustrate the speed and memory improvements from using KeOps over vanilla PyTorch on the GPU (1x RTX 2080 Ti) for both the standard MMD and learned kernel MMD detectors.
Data
We randomly sample points from the standard normal distribution and run the detectors with PyTorch and KeOps backends for the following settings:
\(N_\text{ref}, N_\text{test} = [2, 5, 10, 20, 50, 100]\) (batch sizes in ‘000s)
\(D = [2, 10, 50]\)
Where \(D\) denotes the number of features.
Requirements
The notebook requires PyTorch and KeOps to be installed. Once PyTorch is installed, KeOps can be installed via pip:
[ ]:
!pip install pykeops
Before we start let’s fix the random seeds for reproducibility:
[1]:
import numpy as np
import torch
def set_seed(seed: int) -> None:
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
np.random.seed(seed)
set_seed(2022)
Vanilla PyTorch vs. KeOps comparison
Utility functions
First we define some utility functions to run the experiments:
[2]:
from alibi_detect.cd import MMDDrift, LearnedKernelDrift
from alibi_detect.utils.keops.kernels import DeepKernel as DeepKernelKeops
from alibi_detect.utils.keops.kernels import GaussianRBF as GaussianRBFKeops
from alibi_detect.utils.pytorch.kernels import DeepKernel as DeepKernelTorch
from alibi_detect.utils.pytorch.kernels import GaussianRBF as GaussianRBFTorch
import matplotlib.pyplot as plt
from scipy.stats import kstest
from timeit import default_timer as timer
import torch.nn as nn
import torch.nn.functional as F
class Projection(nn.Module):
def __init__(self, d_in: int, d_out: int = 2):
super().__init__()
self.lin1 = nn.Linear(d_in, d_out)
self.lin2 = nn.Linear(d_out, d_out)
def forward(self, x):
return self.lin2(F.relu(self.lin1(x)))
def eval_detector(p_vals: np.ndarray, threshold: float, is_drift: bool, t_mean: float, t_std: float) -> dict:
""" In case of drifted data (ground truth) it returns the detector's power.
In case of no drift, it computes the false positive rate (FPR) and whether the p-values
are uniformly distributed U[0,1] which is checked via a KS test. """
results = {'power': None, 'fpr': None, 'ks': None}
below_p_val_threshold = (p_vals <= threshold).mean()
if is_drift:
results['power'] = below_p_val_threshold
else:
results['fpr'] = below_p_val_threshold
stat_ks, p_val_ks = kstest(p_vals, 'uniform')
results['ks'] = {'p_val': p_val_ks, 'stat': stat_ks}
results['p_vals'] = p_vals
results['time'] = {'mean': t_mean, 'stdev': t_std}
return results
def experiment(detector: str, backend: str, n_runs: int, n_ref: int, n_test: int, n_features: int,
mu: float = 0.) -> dict:
""" Runs the experiment n_runs times, each time with newly sampled reference and test data.
Returns the p-values for each test as well as the mean and standard deviations of the runtimes. """
p_vals, t_detect = [], []
for _ in range(n_runs):
# Sample reference and test data
x_ref = np.random.randn(*(n_ref, n_features)).astype(np.float32)
x_test = np.random.randn(*(n_test, n_features)).astype(np.float32) + mu
# Initialise detector, make and log predictions
p_val = .05
dd_kwargs = dict(p_val=p_val, backend=backend, n_permutations=100)
if detector == 'mmd':
dd = MMDDrift(x_ref, **dd_kwargs)
elif detector == 'learned_kernel':
d_out, sigma = 2, .1
proj = Projection(n_features, d_out)
Kernel = GaussianRBFKeops if backend == 'keops' else GaussianRBFTorch
kernel_a = Kernel(trainable=True, sigma = torch.Tensor([sigma]))
kernel_b = Kernel(trainable=True, sigma = torch.Tensor([sigma]))
device = torch.device('cuda')
DeepKernel = DeepKernelKeops if backend == 'keops' else DeepKernelTorch
deep_kernel = DeepKernel(proj, kernel_a, kernel_b, eps=.01).to(device)
if backend == 'pytorch' and n_ref + n_test > 20000:
batch_size = 10000
batch_size_predict = 10000
else:
batch_size = 1000000
batch_size_predict = 1000000
dd_kwargs.update(
dict(
epochs=2, train_size=.75, batch_size=batch_size, batch_size_predict=batch_size_predict
)
)
dd = LearnedKernelDrift(x_ref, deep_kernel, **dd_kwargs)
start = timer()
pred = dd.predict(x_test)
end = timer()
if _ > 0: # first run reserved for KeOps compilation
t_detect.append(end - start)
p_vals.append(pred['data']['p_val'])
del dd, x_ref, x_test
torch.cuda.empty_cache()
p_vals = np.array(p_vals)
t_mean, t_std = np.array(t_detect).mean(), np.array(t_detect).std()
results = eval_detector(p_vals, p_val, mu != 0., t_mean, t_std)
return results
def format_results(experiments: dict, n_features: list, backends: list, max_batch_size: int = 1e10) -> dict:
T = {'batch_size': None, 'keops': None, 'pytorch': None}
T['batch_size'] = np.unique([experiments['keops'][_]['n_ref'] for _ in experiments['keops'].keys()])
T['batch_size'] = list(T['batch_size'][T['batch_size'] <= max_batch_size])
T['keops'] = {f: [] for f in n_features}
T['pytorch'] = {f: [] for f in n_features}
for backend in backends:
for f in T[backend].keys():
for bs in T['batch_size']:
for k, v in experiments[backend].items():
if f == v['n_features'] and bs == v['n_ref']:
T[backend][f].append(results[backend][k]['time']['mean'])
for k, v in T['keops'].items(): # apply padding
n_pad = len(v) - len(T['pytorch'][k])
T['pytorch'][k] += [np.nan for _ in range(n_pad)]
return T
def plot_absolute_time(experiments: dict, results: dict, n_features: list, y_scale: str = 'linear',
detector: str = 'MMD', max_batch_size: int = 1e10):
T = format_results(experiments, n_features, ['keops', 'pytorch'], max_batch_size)
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'b']
legend, n_c = [], 0
for f in n_features:
plt.plot(T['batch_size'], T['keops'][f], linestyle='solid', color=colors[n_c]);
legend.append(f'keops - {f}')
plt.plot(T['batch_size'], T['pytorch'][f], linestyle='dashed', color=colors[n_c]);
legend.append(f'pytorch - {f}')
n_c += 1
plt.title(f'{detector} drift detection time for 100 permutations')
plt.legend(legend, loc=(1.1,.1));
plt.xlabel('Batch size');
plt.ylabel('Time (s)');
plt.yscale(y_scale);
plt.show();
def plot_relative_time(experiments: dict, results: dict, n_features: list, y_scale: str = 'linear',
detector: str = 'MMD', max_batch_size: int = 1e10):
T = format_results(experiments, n_features, ['keops', 'pytorch'], max_batch_size)
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'b']
legend, n_c = [], 0
for f in n_features:
t_keops, t_torch = T['keops'][f], T['pytorch'][f]
ratio = [tt / tk for tt, tk in zip(t_torch, t_keops)]
plt.plot(T['batch_size'], ratio, linestyle='solid', color=colors[n_c]);
legend.append(f'pytorch/keops - {f}')
n_c += 1
plt.title(f'{detector} drift detection pytorch/keops time ratio for 100 permutations')
plt.legend(legend, loc=(1.1,.1));
plt.xlabel('Batch size');
plt.ylabel('time pytorch / keops');
plt.yscale(y_scale);
plt.show();
As detailed earlier, we will compare the PyTorch with the KeOps implementation of the MMD and learned kernel MMD detectors for a variety of reference and test data batch sizes as well as different feature dimensions. Note that for the PyTorch implementation, the portion of the kernel matrix for the reference data itself can already be computed at initialisation of the detector. This computation will not be included when we record the detector’s prediction time. Since use cases where \(N_\text{ref} >> N_\text{test}\) are quite common, we will also test for this specific setting. The key reason is that we cannot amortise this computation for the KeOps detector since we are working with lazily evaluated symbolic matrices.
MMD detector
1. \(N_\text{ref} = N_\text{test}\)
Note that for KeOps we could further increase the number of instances in the reference and test sets (e.g. to 500,000) without running into memory issues.
[3]:
experiments_eq = {
'keops': {
0: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 5, 'n_features': 2},
1: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 5, 'n_features': 2},
2: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 5, 'n_features': 2},
3: {'n_ref': 20000, 'n_test': 20000, 'n_runs': 5, 'n_features': 2},
4: {'n_ref': 50000, 'n_test': 50000, 'n_runs': 5, 'n_features': 2},
5: {'n_ref': 100000, 'n_test': 100000, 'n_runs': 5, 'n_features': 2},
6: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 5, 'n_features': 10},
7: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 5, 'n_features': 10},
8: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 5, 'n_features': 10},
9: {'n_ref': 20000, 'n_test': 20000, 'n_runs': 5, 'n_features': 10},
10: {'n_ref': 50000, 'n_test': 50000, 'n_runs': 5, 'n_features': 10},
11: {'n_ref': 100000, 'n_test': 100000, 'n_runs': 5, 'n_features': 10},
12: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 5, 'n_features': 50},
13: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 5, 'n_features': 50},
14: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 5, 'n_features': 50},
15: {'n_ref': 20000, 'n_test': 20000, 'n_runs': 5, 'n_features': 50},
16: {'n_ref': 50000, 'n_test': 50000, 'n_runs': 5, 'n_features': 50},
17: {'n_ref': 100000, 'n_test': 100000, 'n_runs': 5, 'n_features': 50}
},
'pytorch': { # runs OOM after 10k instances in ref and test sets
0: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 5, 'n_features': 2},
1: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 5, 'n_features': 2},
2: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 5, 'n_features': 2},
3: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 5, 'n_features': 10},
4: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 5, 'n_features': 10},
5: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 5, 'n_features': 10},
6: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 5, 'n_features': 50},
7: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 5, 'n_features': 50},
8: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 5, 'n_features': 50}
}
}
[4]:
backends = ['keops', 'pytorch']
results = {backend: {} for backend in backends}
for backend in backends:
exps = experiments_eq[backend]
for i, exp in exps.items():
results[backend][i] = experiment(
'mmd', backend, exp['n_runs'], exp['n_ref'], exp['n_test'], exp['n_features']
)
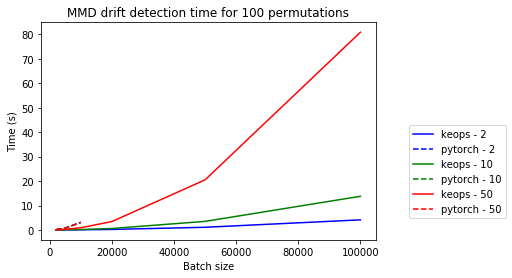
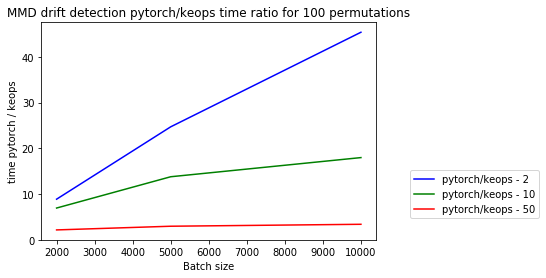
Below we visualise the runtimes of the different experiments. We can make the following observations:
The relative speed improvements of KeOps over vanilla PyTorch increase with increasing batch size.
Due to the explicit kernel computation and storage, the PyTorch detector runs out-of-memory after a little over 10,000 instances in each of the reference and test sets while KeOps keeps scaling up without any issues.
The relative speed improvements decline with growing feature dimension. Note however that we would not recommend using a (untrained) MMD detector on very high-dimensional data in the first place.
The plots show both the absolute and relative (PyTorch / KeOps) mean prediction times for the MMD drift detector for different feature dimensions \([2, 10, 50]\).
[5]:
n_features = [2, 10, 50]
max_batch_size = 100000
plot_absolute_time(experiments_eq, results, n_features, max_batch_size=max_batch_size)
[6]:
plot_relative_time(experiments_eq, results, n_features, max_batch_size=max_batch_size)
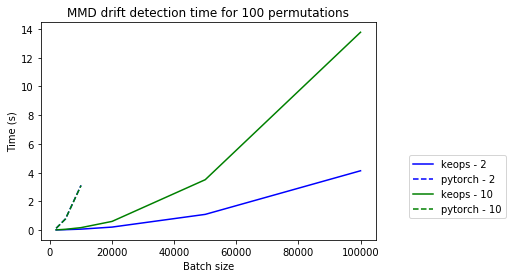
The difference between KeOps and PyTorch is even more striking when we only look at \([2, 10]\) features:
[7]:
plot_absolute_time(experiments_eq, results, [2, 10], max_batch_size=max_batch_size)
2. \(N_\text{ref} >> N_\text{test}\)
Now we check whether the speed improvements still hold when \(N_\text{ref} >> N_\text{test}\) (\(N_\text{ref} / N_\text{test} = 10\)) and a large part of the kernel can already be computed at initialisation time of the PyTorch (but not the KeOps) detector.
[8]:
experiments_neq = {
'keops': {
0: {'n_ref': 2000, 'n_test': 200, 'n_runs': 10, 'n_features': 2},
1: {'n_ref': 5000, 'n_test': 500, 'n_runs': 10, 'n_features': 2},
2: {'n_ref': 10000, 'n_test': 1000, 'n_runs': 10, 'n_features': 2},
3: {'n_ref': 20000, 'n_test': 2000, 'n_runs': 10, 'n_features': 2},
4: {'n_ref': 50000, 'n_test': 5000, 'n_runs': 10, 'n_features': 2},
5: {'n_ref': 100000, 'n_test': 10000, 'n_runs': 10, 'n_features': 2}
},
'pytorch': {
0: {'n_ref': 2000, 'n_test': 200, 'n_runs': 10, 'n_features': 2},
1: {'n_ref': 5000, 'n_test': 500, 'n_runs': 10, 'n_features': 2},
2: {'n_ref': 10000, 'n_test': 1000, 'n_runs': 10, 'n_features': 2}
}
}
[9]:
results = {backend: {} for backend in backends}
for backend in backends:
exps = experiments_neq[backend]
for i, exp in exps.items():
results[backend][i] = experiment(
'mmd', backend, exp['n_runs'], exp['n_ref'], exp['n_test'], exp['n_features']
)
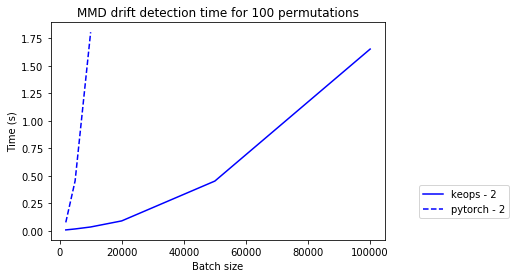
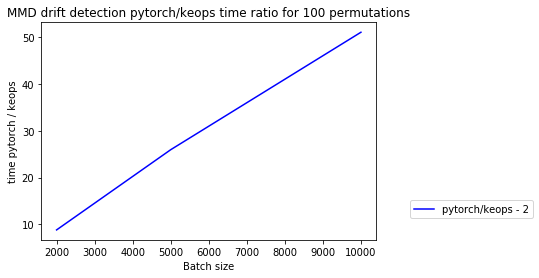
The below plots illustrate that KeOps indeed still provides large speed ups over PyTorch. The x-axis shows the reference batch size \(N_\text{ref}\). Note that \(N_\text{ref} / N_\text{test} = 10\).
[10]:
plot_absolute_time(experiments_neq, results, [2], max_batch_size=max_batch_size)
[11]:
plot_relative_time(experiments_neq, results, [2], max_batch_size=max_batch_size)
Learned kernel MMD detector
We conduct similar experiments as for the MMD detector for \(N_\text{ref} = N_\text{test}\) and n_features=50. We use a deep learned kernel with an MLP followed by Gaussian RBF kernels and project the input features on a d_out=2-dimensional space. Since the learned kernel detector computes the kernel matrix in a batch-wise manner, we can also scale up the number of instances for the PyTorch backend without running out-of-memory.
[12]:
experiments_eq = {
'keops': {
0: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 3, 'n_features': 50},
1: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 3, 'n_features': 50},
2: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 3, 'n_features': 50},
3: {'n_ref': 20000, 'n_test': 20000, 'n_runs': 3, 'n_features': 50},
4: {'n_ref': 50000, 'n_test': 50000, 'n_runs': 3, 'n_features': 50},
5: {'n_ref': 100000, 'n_test': 100000, 'n_runs': 3, 'n_features': 50}
},
'pytorch': {
0: {'n_ref': 2000, 'n_test': 2000, 'n_runs': 3, 'n_features': 50},
1: {'n_ref': 5000, 'n_test': 5000, 'n_runs': 3, 'n_features': 50},
2: {'n_ref': 10000, 'n_test': 10000, 'n_runs': 3, 'n_features': 50},
3: {'n_ref': 20000, 'n_test': 20000, 'n_runs': 3, 'n_features': 50},
4: {'n_ref': 50000, 'n_test': 50000, 'n_runs': 3, 'n_features': 50},
5: {'n_ref': 100000, 'n_test': 100000, 'n_runs': 3, 'n_features': 50}
}
}
[13]:
results = {backend: {} for backend in backends}
for backend in backends:
exps = experiments_eq[backend]
for i, exp in exps.items():
results[backend][i] = experiment(
'learned_kernel', backend, exp['n_runs'], exp['n_ref'], exp['n_test'], exp['n_features']
)
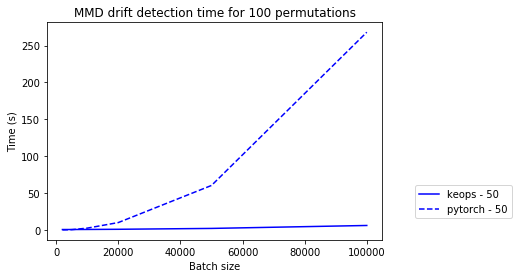
We again plot the absolute and relative (PyTorch / KeOps) mean prediction times for the learned kernel MMD drift detector for different feature dimensions:
[14]:
max_batch_size = 100000
plot_absolute_time(experiments_eq, results, [50], max_batch_size=max_batch_size)
[15]:
plot_relative_time(experiments_eq, results, [50], max_batch_size=max_batch_size)
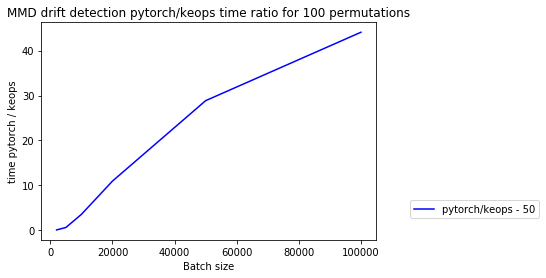
Conclusion
As illustrated in the experiments, KeOps allows you to drastically speed up and scale up drift detection to larger datasets without running into memory issues. The speed benefit of KeOps over the PyTorch (or TensorFlow) MMD detectors decrease as the number of features increases. Note though that it is not advised to apply the (untrained) MMD detector to very high-dimensional data in the first place and that we can apply dimensionality reduction via the deep kernel for the learned kernel MMD detector.